
Рис. 3.1
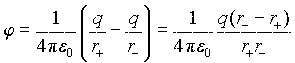
Если расстояние l между зарядами мало по сравнению с расстоянием до точки P, то такая система зарядов называется диполем. Учитывая, что l<<r, можно приближенно положить:
![]()
Тогда потенциал диполя равен
| Лекция 3. | Диполь. Мультипольное разложение. Диполь во внешнем электрическом поле. |
Найдем потенциал, создаваемый в точке P(r) двумя равными по величине зарядами противоположных знаков, расположенными на небольшом расстоянии друг от друга вблизи начала координат.
 Рис. 3.1 |
Если расстояние l между зарядами мало по сравнению с расстоянием до точки P, то такая система зарядов называется диполем. Учитывая, что l<<r, можно приближенно положить:
Тогда потенциал диполя равен |
 |
(3.1) |
где обозначено ql=p или
 |
(3.2) |
где вектор p определен как p=ql и называется электрическим моментом диполя или дипольным моментом.
Найдем в полярной системе координат компоненты Er и Eq вектора напряженности поля, создаваемого диполем. Для этого воспользуемся известной связью между напряженностью поля и потенциалом:
Выразим оператор набла в полярной системе координат
Подставляя j из (3.1), будем иметь:
|
 Рис. 3.2 |
Тогда квадрат модуля вектора напряженности равен

а модуль
 |
(3.5) |
Выразим вектор E через радиус вектор r и вектор дипольного момента p. Для этого применим соотношение (3.3) к потенциалу диполя в виде (3.2). Ввиду громоздкости выкладок, найдем вектор E покомпонентно



По аналогии можно получить


Тогда окончательно будем иметь
 |
(3.6) |
Полученное выражение не зависит от системы координат и выражает вектор напряженности поля через известные вектора p и r.
 Рис. 3.3 |
Пусть вблизи начала
координат находится некоторое
количество точечных зарядов.
Определим потенциал поля,
создаваемого этими зарядами в
точке P, расположенной на
большом удалении (по сравнению
с расстояниями между зарядами)
от начала координат. В силу принципа суперпозиции потенциал всей совокупности зарядов равен сумме потенциалов, создаваемых в данной точке поля каждым из зарядов в отдельности:
|
Для определения расстояния от i-того заряда до точки P воспользуемся теоремой косинусов (см. рис. 3.3):

Учитывая, что ri/ro << 1, выражение в скобках можно представить как (1+Δx), где Δx - малая величина, по степеням которой можно сделать разложение в ряд. Ограничиваясь линейными по ri/ro членами, получим следующее выражение:

Тогда для потенциала (3.7) будем иметь

Величина![]() называется
электрическим дипольным моментом
системы зарядов.
называется
электрическим дипольным моментом
системы зарядов.
Окончательно для потенциала системы зарядов, расположенной вблизи начала координат, в удаленной от нее точке, характеризуемой радиус-вектором r, имеем
 |
(3.8) |
Как следует из полученного выражения, при не равном нулю суммарном заряде потенциал определяется в основном первым членом, стоящим в скобках в (3.8), потому что он ~1/r, тогда как второй член ~1/r2. Однако во многих важных случаях суммарный заряд системы равен нулю, как это имеет место, например, для молекулы. Расположение же зарядов может быть таково, что дипольный момент системы отличен от нуля. Тогда потенциал определяется вторым членом. Заметим, что и при равном нулю дипольном моменте потенциал системы, вообще говоря, не равен нулю, а определяется членами высших порядков в разложении по степеням ri/ro. Напомним, что речь все время идет о потенциале в точках, расположенных на большом удалении от системы.
Для диполя из (3.8) легко получается выведенное ранее выражение (3.2).
Найдем момент сил, действующих на диполь в однородном электрическом поле. Пусть положения положительного и отрицательного зарядов относительно центра диполя характеризуются векторами r+ и r- , соответственно. Тогда, в соответствии с определением момента сил, имеем
 Рис. 3.4 |
Так как по определению
|
Момент сил, очевидно, равен нулю, когда векторы p и E коллинеарны, однако устойчивым положением является только такое положение, когда они еще и совпадают по направлению. В однородном поле, очевидно, F+ + F_= 0.
Если диполь находится в неоднородном внешнем электрическом поле, то равнодействующая сил, действующих на положительный и отрицательный заряды диполя оказывается не равной нулю:
 |
(3.10) |
где E+ и E_ - напряженность поля в точках расположения положительного и отрицательного зарядов, соответственно, а разность E+ - E_ есть приращение вектора E на отрезке, равном длине диполя, взятом в направлении его оси. В выражение (3.10) входит так называемая производная вектора по направлению, которая в общем случае определяется довольно сложно. Рассмотрим простейший случай, когда неоднородное поле обладает симметрией относительно оси x. Пусть ось диполя также направлена вдоль оси x. Тогда сила будет иметь составляющую только вдоль оси x, равную

Если, например, поле убывает в направлении оси диполя, то производная в последнем выражении будет отрицательной, и диполь будет втягиваться в область более сильного поля.
Находясь во внешнем поле, диполь обладает некоторой энергией помимо энергии взаимодействия зарядов его составляющих.
 Рис. 3.5 |
Пусть диполь находится в однородном электрическом поле. Направим ось x вдоль вектора E. Поскольку
то потенциальная энергия диполя будет равна |

где a - угол между осью диполя и направлением поля.
| [ наверх ] | [ в оглавление конспекта ] | [ на главную ] |