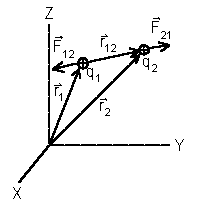
Рис. 1.1
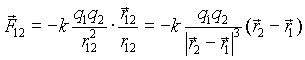 (1.1)
(1.1)
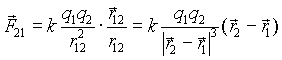 (1.2)
(1.2)
Здесь k - множитель,
зависящий от выбранной системы
единиц. В системе СИ его
принято записывать как 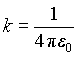 ,
где
,
где ![]()
Лекция1. |
Свойства заряда. Закон Кулона. Электрическое поле. Потенциал. Связь между напряженностью электрического поля и потенциалом. |
- заряды одного вида отталкиваются друг от друга, заряды разных видов - притягиваются, причем сила отталкивания равна по модулю силе притягивания;
- число положительных и отрицательных зарядов во Вселенной одинаковое.
- минимальный заряд частицы e = 1.60·10-19 Кл;
- любой заряд q кратен минимальному, т.е. q=Ne, где N - целое число;
- минимальные положительный и отрицательный заряды равны по абсолютной величине.
Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей заряды прямой.
Рис. 1.1 |
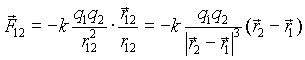 (1.1) (1.1)
Здесь k - множитель,
зависящий от выбранной системы
единиц. В системе СИ его
принято записывать как |
Закон Кулона установлен экспериментально, но его справедливость подтверждается и тем, что с опытом согласуются все выводы теории, в основе которой лежит этот закон.
Как показывает опыт, сила взаимодействия двух зарядов не изменяется при наличии третьего заряда. Поэтому, независимо от числа зарядов выражения (1.1)-(1.2) можно использовать для вычисления силы взаимодействия каждой пары. Тогда при наличии многих зарядов сила, действующая на заряд 1 со стороны всех остальных зарядов есть
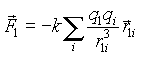 (1.3)
(1.3)
Заряд изменяет свойства окружающего его пространства, т.е. он создает вокруг себя нечто материальное, посредством чего осуществляется взаимодействие между зарядами. Это нечто и называется электрическим полем. Для обнаружения и исследования электрического поля нужно воспользоваться пробным зарядом. Пробный заряд должен быть точечным и малым (чтобы не искажать поле своим присутствием). Поле характеризуется величиной напряженности, которая численно равна силе, действующей на единичный пробный заряд:
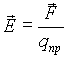 (1.4)
(1.4)
Направление вектора напряженности совпадает с направлением силы, действующей на положительный заряд.
В математике вводится определение векторного поля как части пространства, каждой точке которого сопоставлен вектор. Так совокупность векторов E образует поле вектора напряженности электрического поля. Графически поле E изображается при помощи силовых линий напряженности.
Из (1.3)-(1.4) следует, что напряженность поля системы зарядов равна векторной сумме напряженности полей, которые создавал бы каждый из зарядов системы в отдельности:
![]() (1.5)
(1.5)
Это положение называется принципом суперпозиции. Следует отметить, что выражение (1.5) отнюдь не тривиально, а выражает собой закон природы.
Принцип суперпозиции позволяет вычислить напряженность поля любой системы зарядов. Пусть имеется N точечных зарядов разных знаков, расположенных в точках пространства, с радиус-векторами ri . Требуется найти поле в точке с радиус-вектором ro . Тогда, так как rio = ro-ri , то результирующее поле будет равно:
Рис. 1.2 |
Заряды qi подставляются в (1.6) со своими знаками. Если заряды не точечные, то их разбивают на малые доли dq, которые могут считаться точечными и тогда
где интегрирование производится по всей области распределения заряда. |
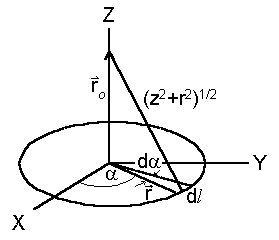 Рис. 1.3 |
Пусть, например,
имеется равномерно заряженное
кольцо радиуса r с полным
зарядом q и требуется
найти напряженность поля E
в произвольной точке на его оси
(Рис. 1.3). Разобъем кольцо на бесконечно малые участки dl, на каждый из которых приходится заряд dq, равный:
Введем систему координат, как показано на рис. 1.3. Радиусы векторы точки наблюдения и элемента dl равны, соответственно:
|
В силу симметрии распределения заряда проекции Ex и Ey вектора E в любой точке на оси кольца должны быть равны нулю. Тогда E= Ez k. Проекцию Ez найдем по формуле (1.7):
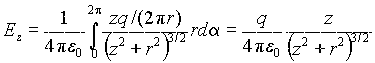
Равенство нулю проекций Ex и Ey можно получить и чисто формально из (1.7):
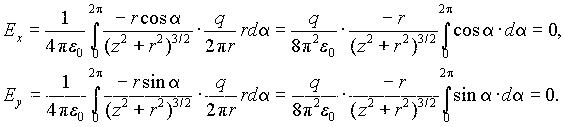
Поскольку электростатическое поле является центральным, то оно консервативно. Работа по перемещению пробного заряда q' из точки 1 в точку 2 не зависит от пути и выражается, как
Для центральной силы ![]() ,
потому что сила направлена вдоль
радиуса, и проекция dl на
направление силы дает приращение
модуля радиус-вектора.
,
потому что сила направлена вдоль
радиуса, и проекция dl на
направление силы дает приращение
модуля радиус-вектора.
Тогда
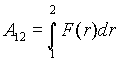 (1.9)
(1.9)
Для кулоновской силы, действующей на пробный заряд q' со стороны точечного заряда q, имеем
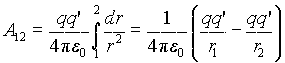 (1.10)
(1.10)
Работа сил консервативного поля может быть представлена как убыль потенциальной энергии Wp при переходе от точки 1 к точке 2:
| A12=Wp1-Wp2 | (1.11) |
Тогда потенциальная энергия заряда q' в поле заряда q есть
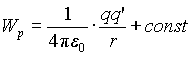 (1.12)
(1.12)
Выбирая константу так,
чтобы Wp = 0 при ![]() ,
имеем
,
имеем
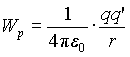 (1.13)
(1.13)
Величина 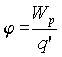 называется потенциалом. Потенциал
численно равен потенциальной
энергии, которой обладал бы в
данной точке поля положительный
единичный заряд. Работа по переносу
заряда q из точки 1 в точку 2
может быть записана как
называется потенциалом. Потенциал
численно равен потенциальной
энергии, которой обладал бы в
данной точке поля положительный
единичный заряд. Работа по переносу
заряда q из точки 1 в точку 2
может быть записана как
![]() (1.14)
(1.14)
Тогда, так как потенциал на бесконечности положен равным нулю то можно сказать, что потенциал равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.
Единицей потенциала является Вольт. 1В - это потенциал в такой точке, для перемещения в которую из бесконечности заряда в 1Кл нужно затратить работу в 1Дж.
В силу принципа суперпозиции потенциал поля, создаваемого системой зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности:
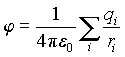 (1.15)
(1.15)
Если заряд распределен непрерывно с объемной плотностью ρ(r), то, переходя в (1.15) от суммирования к интегрированию по бесконечно малым зарядам ρdV, получим
 |
(1.16) |
Как известно, в потенциальном поле сила может быть получена из потенциальной энергии из соотношения
![]() (1.17)
(1.17)
Тогда для напряженности электрического поля из соотношений
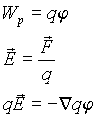
![]() (1.18)
(1.18)
С другой стороны, из соотношений (1.8) и (1.14) следует, что
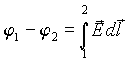 (1.19)
(1.19)
Поверхности равного
потенциала, т.е. такие поверхности,
на которых ![]() называются
эквипотенциальными. При
перемещении заряда вдоль
эквипотенциальной поверхности
работа, производимая силами поля,
равна нулю. Но при не равной нулю
силе это означает, что сила
перпендикулярна перемещению.
Поэтому можно утверждать, что
напряженность электрического поля
в каждой точке пространства
перпендикулярна эквипотенциальной
поверхности, проходящей через эту
точку. Иначе говоря, силовые
линии перпендикулярны
эквипотенциальным поверхностям.
называются
эквипотенциальными. При
перемещении заряда вдоль
эквипотенциальной поверхности
работа, производимая силами поля,
равна нулю. Но при не равной нулю
силе это означает, что сила
перпендикулярна перемещению.
Поэтому можно утверждать, что
напряженность электрического поля
в каждой точке пространства
перпендикулярна эквипотенциальной
поверхности, проходящей через эту
точку. Иначе говоря, силовые
линии перпендикулярны
эквипотенциальным поверхностям.
| [ наверх ] | [ в оглавление конспекта ] | [ на главную ] |