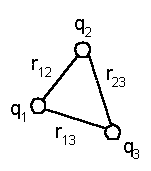
Рис. 6.1
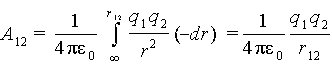 |
(6.1) |
| Лекция 6. | Энергия системы зарядов. Энергия заряженного проводника. Энергия заряженного конденсатора. Энергия электрического поля. Энергия системы двух заряженных тел. |
Потенциальная энергия Wp неподвижной системы зарядов представляет собой работу, необходимую для создания этой системы из отдельных частей, т.е. энергию, запасенную в созданной системе. Это - скалярная величина, являющаяся свойством системы в целом.
 Рис. 6.1 |
Соберем систему из
трех зарядов, последовательно
перенося их из бесконечности в
данные точки пространства, как
показано на рис. 6.1. При
переносе первого заряда в
пространстве, где отсутствует
электрическое поле, сила на
заряд не действует, и работа не
совершается. При переносе
второго заряда работа составит
(см. 1.9)
|
Поскольку r изменяется от бесконечности до r12, то dr в (6.1) отрицательно. Очевидно, что работа, произведенная над системой, будет положительной для одноименных зарядов, так как они отталкиваются.
Перенос третьего заряда будет осуществляться в поле двух зарядов. На основании принципа суперпозиции это поле есть сумма полей, создаваемых каждым из зарядов. Тогда работа, производимая внешними силами над третьим зарядом будет равна сумме двух работ, одна из которых необходима для переноса заряда q3, если имеется только один заряд q1, а другая требуется для переноса заряда q3 при наличии только одного заряда q2
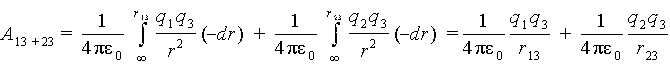 |
(6.2) |
Следовательно, потенциальная энергия системы из трех зарядов, равная полной работе, затраченной на образование указанного на рис.6.1 расположения зарядов, составит
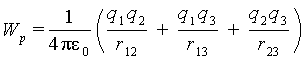 |
(6.3) |
Нетрудно видеть, что полученный результат не зависит от порядка переноса зарядов.
Как всегда в определении потенциальной энергии существует некоторый произвол. В данном случае нулевое значение потенциальной энергии соответствует ситуации, когда все три заряда находятся на беконечно больших расстояниях друг от друга.
Очевидно, что если система состоит из N зарядов, то в выражении (6.3) будет N слагаемых того же вида. Один из способов написания такой суммы по парам зарядов следующий
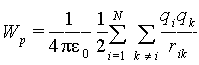 |
(6.4) |
Знак двойной суммы в (6.4) обозначает: возьмите i=1 и суммируйте по k=2,3,4,...,N; затем возьмите i=2 и суммируйте по k=1,3,4,...N; и т.д. до i=N. Ясно, что при этом каждая пара войдет в сумму дважды, поэтому перед знаком суммы стоит множитель 1/2.
На основании (1.15) потенциальную энергию (6.4) системы зарядов можно представить следующим образом
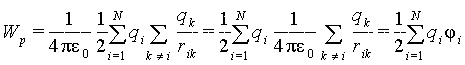 |
(6.5) |
где φi - потенциал, создаваемый всеми зарядами кроме qi , в той точке, где помещается заряд qi .
Обобщение полученного выражения (6.5) на случай непрерывного распределения заряда с объемной плотностью ρ производится аналогично переходу от (1.15) к (1.16):
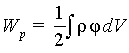 |
(6.6) |
Как известно, заряд сосредоточивается на поверхности проводника, причем поверхность проводника эквипотенциальна. Разбивая эту поверхность на маленькие участки, каждый из которых имеет заряд Δq, и учитывая, что потенциал в месте расположения каждого из зарядов одинаков, имеем
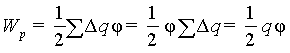 |
(6.7) |
Так как емкость проводника C=q/φ , то выражение (6.7) может быть также представлено, как
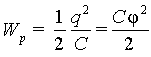 |
(6.8) |
Пусть заряд +q находится на обкладке с потенциалом φ1 а заряд -q на обкладке с потенциалом φ2. Тогда на основании тех же рассуждений, которые привели к выражению (6.7), получим
| (6.9) |
где U - разность потенциалов на обкладках конденсатора. Аналогично переходу от (6.7) к (6.8) выражение для энергии конденсатора может быть представлено также в виде
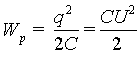 |
(6.10) |
Выражение для энергии в виде (6.6) можно истолковать так. Потенциальная энергия заряда ρdV равна произведению этого заряда на потенциал в той же точке. Вся энергия поэтому получается интегрированием по всему заряду. Оказывается, однако, что энергию можно выразить также и через величину, характеризующую само электрическое поле, - через напряженность E.
Согласно уравнению
Пуассона 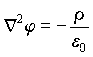 . Выразим отсюда ρ и подставим в (6.6)
. Выразим отсюда ρ и подставим в (6.6)
| (6.11) |
Распишем подинтегральное выражение следующим образом
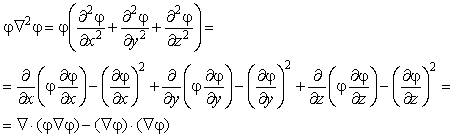 |
(6.12) |
Тогда (6.11) перепишется, как
| (6.13) |
Преобразуем второй интеграл в (6.13) при помощи теоремы Остроградского -Гаусса из объемного в поверхностный
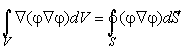 |
(6.14) |
Возьмем поверхность, которая простирается до бесконечности, так что интеграл по объему обращается в интеграл по всему пространству. Пусть выбранная поверхность имеет форму сферы с центром в начале координат и стремящимся к бесконечности радиусом. Потенциал φ изменяется с радиусом как 1/R, а grad φ как 1/R2. Площадь же поверхности сферы растет как R2. Таким образом интеграл по поверхности убывает с ростом радиуса как (1/R)(1/R2)R2=(1/R). Итак, если интегрирование ведется по всему пространству, то поверхностный интеграл обратится в нуль и окончательно получим
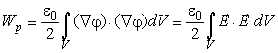 |
(6.15) |
Последнее соотношение можно толковать, говоря, что в том месте пространства, где присутствует электрическое поле, состредоточена и энергия, а плотность ее (количество энергии в единице объема) равна
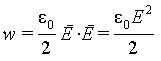 |
(6.16) |
Если пространство заполнено изотропным диэлектриком, то выражение для плотности энергии будет иметь вид
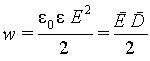 |
(6.17) |
Рассмотрим в качестве примера плоский конденсатор. Его энергия может быть представлена через заряд на обкладках согласно (6.9). Однако можно выразить его энергию и через поле между обкладками. Емкость плоского конденсатора равна
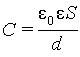 |
(6.18) |
Подставим (6.18) в (6.10) и получим
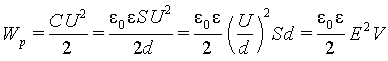 |
(6.19) |
где V - объем пространства между пластинами. Откуда для плотности энергии получается выражение совпадающее с (6.17).
Где же в действительности локализована энергия - там, где заряд, (в данном случае на обкладках конденсатора) или там где, поле, (т.е. в зазоре между обкладками)? В рамках электростатики дать ответ на этот вопрос невозможно.
Меняющиеся во времени поля могут существовать независимо от возбудивших их зарядов, откуда следует, что носителем энергии является поле. Рассмотрим, например, случай, когда движущиеся в антенне заряды возбуждают электромагнитные волны, которые, достигнув антенны приемника, приводят в движение заряды в его антенне. Передача сигнала при этом очевидно связана с передачей энергии. Электромагнитные волны распространяются с конечной скоростью, и им требуется некоторое время, чтобы покрыть расстояние от передатчика до приемника. Заряды в передающей антенне при этом уже не движутся, а в приемной еще не движутся. Очевидно, что энергия должна сохраняться во все моменты, в том числе и в этот промежуток времени. Остается сделать заключение, что энергия в этот промежуток времени локализована в электромагнитном поле волны. Движение зарядов в антенне начнется с приходом волны в ту точку, где расположен приемник, и это движение будет связано с электромагнитной энергией, принесенной волной.
Рассмотрим роль диэлектрика при определении плотности энергии. Представим (6.17) как
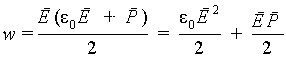 |
(6.20) |
Первое из слагаемых в правой части совпадает с (6.16) и является, таким образом, плотностью энергии электрического поля в вакууме. Покажем, что второе слагаемое представляет собой энергию, затрачиваемую на поляризацию единицы объема диэлектрика. Выразим работу при поляризации единицы объема диэлектрика как
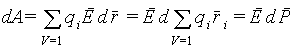 |
(6.21) |
Так как P = κε0E, то dP = κε0dE и dA =κε0EdE. Представим dA как
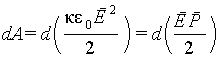 |
(6.22) |
Откуда
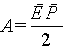 |
(6.23) |
что и требовалось показать.
Представим себе систему из двух заряженных тел в вакууме. Пусть одно тело создает в окружающем пространстве поле E1, а другое - поле E2, так что результирующее поле E обоих тел равно
| (6.24) |
и
| (6.25) |
Полная энергия системы найдется как интеграл по всему пространству от плотности энергии (6.16)
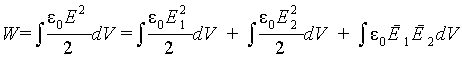 |
(6.26) |
Первые два интеграла в правой части (6.26) представляют собой собственную энергию первого и второго тела, соответственно, а третье слагаемое есть их взаимная энергия. Суммарная положительная собственная энергия тел всегда больше (или равна) их взаимной энергии, могущей иметь как положительные, так и отрицательные значения. Как видно из (6.26) энергия электрического поля не обладает свойством аддитивности, т.е. энергия поля E, являющегося суммой полей E1 и E2, вообще говоря не равна сумме энергий слагаемых полей.
| [ наверх ] | [ в оглавление конспекта ] | [ на главную ] |